
どーも!
たかぽんです!
今回はLeetCodeのSqrt(x)を解きました!
三日坊主脱出です...!
Sqrt(x)
簡単に解説です。
読んで字のごとく、その数xの平方根を求める問題です。
ただし、少数の値が出てきた場合は全て切り捨てて、整数部のみ返します。
以下が公式の例ですが、4の場合は2, 8の場合は2.82842ですが、少数が切り捨てされるため、結局2を返せばOKです。
Input: x = 4
Output: 2
Input: x = 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since the decimal part is truncated, 2 is returned.アルゴリズム
さて、アルゴリズムですが...
これはぱっと見で簡単そうですね。
そもそも大抵のライブラリではすでにルートを出すメソッドがあると思うので、それにて平方根を出します。
すると、2や2.82842といった値が取得できるため、それに対して少数以下の数字を切り捨てる作業をしてあげれば大丈夫なはずです。
ただ...
おそらく、本来はこのsqrtメソッド部分も考えて欲しいのだろうな...?
とおもうので、そちらも考えておこうと思います。
ちょっと詳細を書くのは難しいのですが...
ニュートン法と言うもので解いていくのが一般的なようですね。
すごいざっくり解説すると...
f(x) = x^2-aという関数を考えると、その正のx座標との交点は(√a, 0)になるため、その性質を利用して考えます。
その際、√aより大きなbという数値を考えると、x=bとf(x)の交点から接線を引くと、その線とx軸との交点のx座標は必ず√a<交点のx座標<bとなります。
なので、今度はこの交点の座標をbとして、再度別の接線の交点を求めてあげて〜というのをループすればいつかは√aとほぼ近づくといえます。
わかりづらいと思いますが...以下手書きで試した際のものを貼っておきます。
最終的にはb^2+a/2bと言う値を次の接戦を求める際のb(x座標の値)として使ってあげればいい感じです。
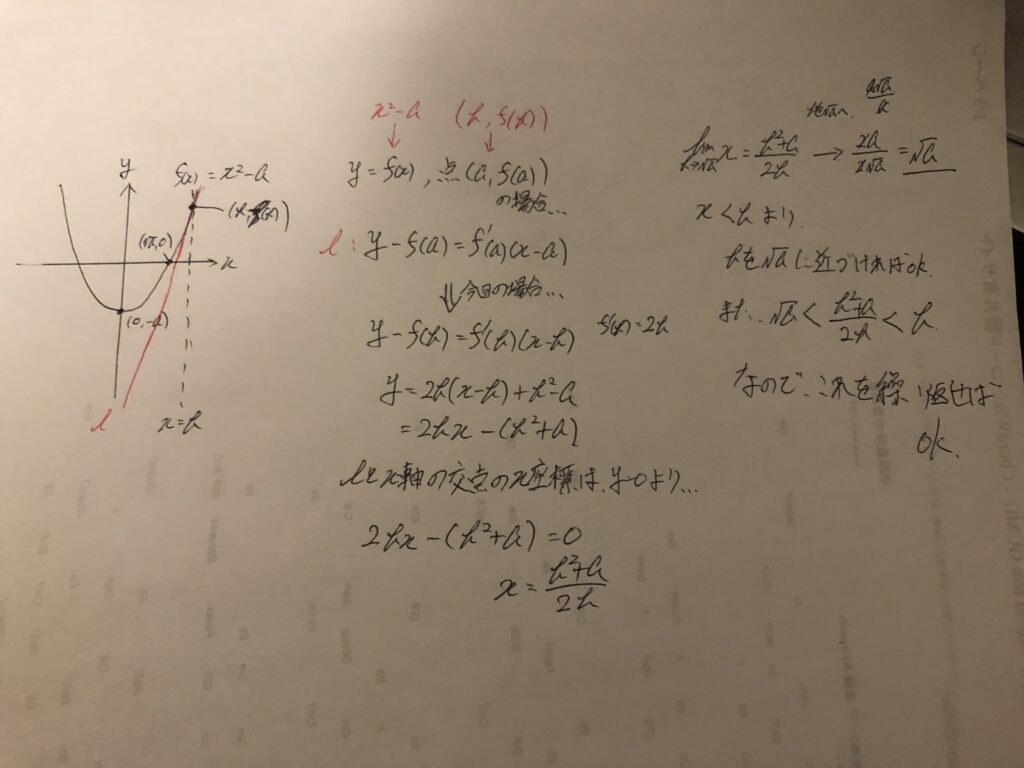
今回はちょっと簡単でしたが、次章に筆者が提出したコードを記載しておきます。
提出コード
今回はなんと一発でいけました...
floorメソッドやsqrtメソッド多少使い方違うかも?と思いましたが、やっぱり言語間で便利関数の使い方を合わせてもらえると知らなくても想像でいけるので助かりますね...!
Runtime: 32 ms, faster than 83.72% of Python3 online submissions for Sqrt(x).
Memory Usage: 14.1 MB, less than 71.69% of Python3 online submissions for Sqrt(x).class Solution:
def mySqrt(self, x: int) -> int:
return floor(sqrt(x))解けたのはいいけど、多分これはずるなので...w
ニュートン法でのものも貼っておきます。
Runtime: 40 ms, faster than 46.27% of Python3 online submissions for Sqrt(x).
Memory Usage: 14.3 MB, less than 42.80% of Python3 online submissions for Sqrt(x).class Solution:
def mySqrt(self, x: int) -> int:
b = x
before = 0
while before != b :
before = b
b = (b * b + x) / (2 * b);
if abs(b - before) < 0.1:
break
print(b)
return floor(b)
簡単に解説を。
基本はbに先程のb^2+x(a)/(2*b)を代入する...という計算を前回の計算した接線の値と今回計算した接線の値が等しくなるまで繰り返せばいいだけなのですが...
最終的に平方根の値が算出できるのかな?と思っていたけど、√3だと、うまくいかず、無限にブレる現象が...
おそらく学術的に調べればもっとビシ!っと出せそうですが、今回はあくまで整数部だけ欲しいので、前回の計算した接線の値と今回計算した接線の値がある程度の範囲内に収まっている(今回は整数だけあればいいので、0.1程度にしています)のであれば、それはもう計算の必要ないかな...ということで、処理をやめて値を返しています。
printはなくても動きますが、この値が実際の接線のx座標の変遷をたどるので、置いておきますね。










